L'approximation de Padé d'ordre un fonctionne comme un traducteur mathématique qui comble le fossé entre les retards thermiques physiques et la logique du système de contrôle. Elle aborde les défis techniques de la régulation des fours électriques en convertissant des composants de retard exponentiels complexes, causés par l'inertie thermique et les retards de transmission, en une fonction de transfert linéaire calculable. Cette transformation permet au contrôleur de compenser efficacement les retards de réponse, garantissant ainsi la stabilité et la précision du système.
Les fours électriques industriels possèdent une inertie thermique importante, créant des délais difficiles à gérer pour les algorithmes standards. L'approximation de Padé d'ordre un simplifie ces retards complexes en un format linéaire, permettant au système de contrôle de prédire le comportement de manière fiable et de maintenir une régulation précise de la température.
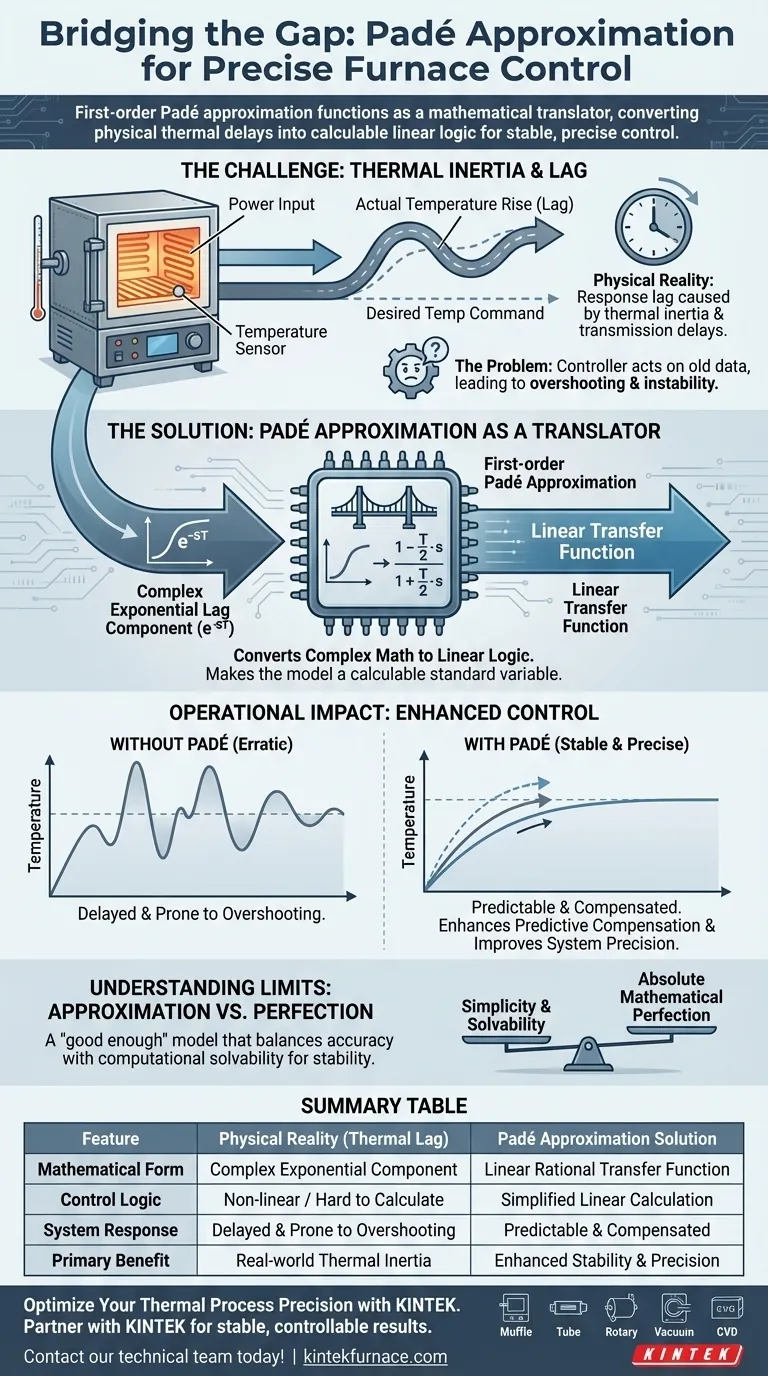
Le Défi : Inertie Thermique et Retard
La Réalité Physique des Fours Électriques
Dans les environnements industriels, les fours électriques ne répondent pas instantanément aux changements de puissance. Il existe toujours un retard de réponse causé par l'inertie thermique et les retards de transmission.
Le Problème des Délais Temporels
Lorsqu'un contrôleur envoie un signal pour augmenter la chaleur, l'augmentation réelle de la température se produit plus tard. Ce délai de transmission crée une déconnexion entre la commande et le résultat.
Sans modélisation appropriée, un contrôleur réagit à des données obsolètes. Cela conduit souvent à un dépassement de la température cible ou à une instabilité du système.
Comment l'Approximation de Padé Résout le Problème
Conversion de Mathématiques Complexes en Logique Linéaire
Mathématiquement, les retards purs sont représentés par des composants de retard exponentiels complexes. Ceux-ci sont difficiles à utiliser directement dans les calculs standards des boucles de contrôle linéaires.
L'approximation de Padé d'ordre un résout ce problème en convertissant le terme exponentiel en une fonction de transfert linéaire. Elle crée une fraction rationnelle mathématique qui approxime le retard.
Rendre le Modèle Calculable
Une fois converti, le retard devient une partie gérable de l'équation du système. L'algorithme de contrôle peut désormais traiter le retard comme une variable standard plutôt qu'une anomalie complexe.
Impact Opérationnel sur le Contrôle de la Température
Amélioration de la Compensation Prédictive
En linéarisant le retard, le contrôleur du four peut prédire de manière plus fiable comment la température réagira au fil du temps. Il peut "voir" le retard venir et ajuster la puissance de sortie à l'avance pour compenser.
Amélioration de la Précision et de la Stabilité du Système
Le résultat final est un système plus robuste. Comme le contrôleur tient compte avec précision de l'inertie thermique, il évite les fluctuations erratiques.
Cela conduit à une précision et une stabilité améliorées pendant le fonctionnement réel, garantissant que le four maintient la bonne température sans oscillations constantes.
Comprendre les Limites de l'Approximation
Approximation vs. Perfection
Il est important de se rappeler que cette méthode est une approximation, pas une réplique exacte du retard physique. Elle simplifie la série infinie d'une fonction exponentielle en un rapport linéaire fini.
Équilibrer Simplicité et Précision
Bien que très efficace pour stabiliser les boucles de four standards, elle sacrifie la perfection mathématique absolue au profit de la résolvabilité computationnelle. Elle fournit un modèle "suffisamment bon" pour assurer la stabilité sans nécessiter une puissance de traitement excessive.
Faire le Bon Choix pour Votre Stratégie de Contrôle
Lors de la conception ou du réglage d'un modèle de contrôle de température pour un four électrique, considérez comment cette approximation s'aligne sur vos objectifs spécifiques.
- Si votre objectif principal est la Stabilité du Système : Utilisez l'approximation de Padé pour éviter les oscillations causées par le décalage entre l'élément chauffant et le capteur.
- Si votre objectif principal est la Simplicité de l'Algorithme : Implémentez cette méthode pour convertir les mathématiques complexes de retard non linéaire en une fonction linéaire standard facile à calculer.
En convertissant le retard physique en une valeur mathématique linéaire, vous transformez une réponse thermique chaotique en un processus prévisible et contrôlable.
Tableau Récapitulatif :
| Caractéristique | Réalité Physique (Retard Thermique) | Solution d'Approximation de Padé |
|---|---|---|
| Forme Mathématique | Composant Exponentiel Complexe | Fonction de Transfert Rationnelle Linéaire |
| Logique de Contrôle | Non linéaire / Difficile à Calculer | Calcul Linéaire Simplifié |
| Réponse du Système | Retardée et Sujette au Dépassement | Prédite et Compensée |
| Bénéfice Principal | Inertie Thermique du Monde Réel | Stabilité et Précision Améliorées |
Optimisez la Précision de Votre Processus Thermique avec KINTEK
Surmonter l'inertie thermique nécessite à la fois une précision mathématique et du matériel haute performance. KINTEK fournit des solutions de chauffage de pointe soutenues par une R&D et une fabrication expertes. Que vous ayez besoin de systèmes Muffle, Tube, Rotatif, sous Vide ou CVD, nos fours haute température de laboratoire sont entièrement personnalisables pour répondre à vos besoins uniques en matière de régulation de température.
Ne laissez pas les retards de réponse compromettre vos résultats. Collaborez avec KINTEK pour obtenir la stabilité et le contrôle dont votre recherche a besoin. Contactez notre équipe technique dès aujourd'hui pour discuter de vos besoins en fours personnalisés !
Guide Visuel
Références
- Serdar Ekinci, Євген Зайцев. Efficient control strategy for electric furnace temperature regulation using quadratic interpolation optimization. DOI: 10.1038/s41598-024-84085-w
Cet article est également basé sur des informations techniques de Kintek Furnace Base de Connaissances .
Produits associés
- 1200℃ Four à atmosphère contrôlée d'azote inerte
- 1700℃ Four à atmosphère contrôlée d'azote inerte
- 1400℃ Four à atmosphère contrôlée d'azote inerte
- 1200℃ Four à tube divisé Four à tube à quartz de laboratoire avec tube à quartz
- Fours de frittage par étincelage et plasma SPS
Les gens demandent aussi
- Quel est l'objectif principal du traitement thermique ? Transformer les propriétés des métaux pour des performances supérieures
- Quelles sont les applications des fours à atmosphère inerte ? Essentiel pour le traitement des métaux, l'électronique et la fabrication additive
- Comment fonctionne un four à atmosphère contrôlée de type batch ? Maîtrisez le traitement thermique de précision pour des matériaux supérieurs
- À quoi sert l'azote dans un four ? Prévenir l'oxydation et contrôler la qualité du traitement thermique
- Quels sont les principaux avantages d'un four à atmosphère de type boîte expérimental ? Obtenez un contrôle environnemental précis pour les matériaux avancés
